Алекс в стране чисел. Необычайное путешествие в волшебный мир математики - Страница 87
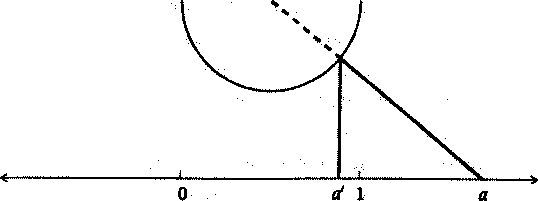
Различие между ℵ0 и c — это различие между числом точек на числовой прямой, представимых в виде дробей, и полным числом точек, включая дроби и иррациональные числа. Однако разрыв между ℵ0 и c столь огромен, что если бы мы наугад выбирали точки на числовой прямой, то вероятность выбрать дробь была бы равна нулю. По сравнению с несчетной бесконечностью иррациональных чисел дробей, можно сказать, попросту очень мало.
С каким бы трудом идеи Кантора ни воспринимались поначалу, история реабилитировала его трактовку числа алеф; не только сам алеф прижился среди чисел практически повсеместно, но и зигзаговые и диагональные доказательства по всеобщему признанию были провозглашены наиболее яркими во всей математике. Давид Гильберт заявил, что «никто не изгонит нас из рая, созданного Кантором».
К несчастью для Кантора, этот рай стоил ему дорого — он заплатил за него своим душевным здоровьем. Поправившись после первого срыва, ученый стал уделять больше внимания другим предметам, таким как теология и история эпохи Елизаветы, и пришел к убеждению, что автором пьес Уильяма Шекспира на самом деле был ученый Фрэнсис Бэкон. Доказательство этой гипотезы стало для Кантора личным крестовым походом, идеей фикс, определявшей его все более странное поведение. В 1911 году Кантора пригласили в Университет Сент-Эндрюс прочитать лекцию по математике. Представ перед публикой, он с жаром принялся обсуждать свои теории о Шекспире и Бэконе, чем немало смутил собравшихся, ожидавших услышать о последних достижениях математической мысли. Кантор испытал еще несколько тяжелых приступов депрессии и много времени проводил в больнице. Умер выдающийся математик в 1918 году.
Набожный лютеранин, Кантор вел широкую переписку с духовными лицами по поводу значимости своих результатов. Он полагал, что его подход к бесконечности продемонстрировал ее постигаемость человеческим разумом, а поэтому подвел человека ближе к Богу. Среди предков Кантора были и евреи, что, как полагают многие, повлияло на его выбор буквы алеф в качестве символа для бесконечности: великий математик мог знать, что в мистической еврейской традиции Каббалы алеф обозначает высшее проявление Бога. Сам же Кантор говорил, что гордится своим выбором алефа, поскольку эта буква, первая буква древнееврейского алфавита, — очень подходящий символ для нового начала.
Алеф годится и для завершения нашего путешествия в мир математики. Эта наука, как я писал в начальных главах этой книги, возникла из стремления человека придать смысл тому, что его окружает. Делая насечки на стволах деревьев или считая на пальцах, наши далекие предки изобрели числа. Числа помогали и в земледелии, и в торговле, они открыли человечеству дверь в «цивилизацию». Затем, по мере развития математики, предметом ее стали в меньшей степени реальные вещи, а в большей — абстракции. Греки ввели в обиход такие концепции, как точка и линия, а индусы изобрели нуль и тем самым проложили дорогу к еще более радикальным абстракциям — отрицательным числам. Хотя эти концепции казались сначала идущими вразрез с интуицией, они довольно быстро были приняты, и ныне мы пользуемся ими ежедневно. К концу XIX столетия, однако, пуповина, связывающая математику с непосредственным опытом, была разорвана раз и навсегда. После Римана и Кантора она потеряла какую-либо связь с интуитивным восприятием мира.
Обнаружив кардинальное число ℵ0, Кантор не остановился и доказал, что имеются даже еще большие бесконечности. Как мы видели, c — это число точек на прямой. Оно же есть число точек на двумерной поверхности. (Еще один удивительный результат, который вам придется принять с моих слов на веру.) Пусть d — число всевозможных кривых, линий и загогулин, которые можно нарисовать на двумерной поверхности. Используя теорию множеств, можно доказать, что d больше, чем с. Можно двинуться и дальше — показать, что должна иметься бесконечность еще бо́льшая, чем d Никто, впрочем, не смог предъявить множество вещей, кардинальное число которого было бы больше, чем d.
Кантор увел нас далеко за пределы вообразимого. Это довольно чудесное место и, занятным образом, противоположное тому, в котором пребывает племя в бассейне Амазонки, о котором говорилось в начале книги. У мундуруку много вещей, но не хватает чисел, чтобы их пересчитать. Кантор предоставил нам числа в неограниченном избытке, зато теперь у нас не хватает вещей, которые можно было пересчитывать с их помощью.
Список литературы
Подробную библиографию по каждой главе, а также приложения можно найти на веб-сайте www.alexbeIlos.com. Ниже перечислены наиболее существенные книги, из которых я почерпнул информацию.
Acheson D. 1089, and All That. New York: Oxford University Press. 2002.
Aczel A. D. Chance. New York: Basic Books, 2005.
Aczel A. D. The Mystery of the Aleph. New York: Washington Square Press, 2000.
Andrews F. E. New Numbers. London: Faber & Faber, 1936. Balliett L. D. The Philosophy of Numbers. Atlantic City, N.J.: L. N. Fowler & Co., 1908.
Beckmann P. A History of Pi. New York: St. Martin’s, 1971.
Bell E. T. Numerology. New York: Century, 1933.
Bell E. T. Men of Mathematics. New York: Touchstone, 1937.
Bennett D. J. Randomness. Cambridge: Harvard University Press. 1998.
Bentley P. J. The Book of Numbers. London: Cassell Illustrated, 2008.
Berggren L., Borwein J., and Borwein P. Pi: A Source Book. New York: Springer, 2003.
Butterworth B. The Mathematical Brain. London: Macmillan, 1999.
Cajori F. A History of Mathematical Notations. New York: Dover, 1993 (facsimile of original by Illinois: Open Court, 1928/9).
Cohen I. B. The Triumph of Numbers. New York: W. W. Norton, 2005.
Darling D. The Universal Book of Mathematics. Hoboken, N.J.: Wiley, 2004.
Dehaene S. The Number Sense. Oxford: Oxford University Press, 1997.
Derbyshire J. Unknown Quantity. London: Atlantic Books, 2006.
Devlin K. All the Math That's Fit to Print. Washington: Mathematical Association of America, 1994.
Dudley U. Numerology. Washington: Mathematical Association of America, 1997.
Dudley U. (ed.). Is Mathematics Inevitable? Washington: Mathematical Association of America, 2008.
Du Sautoy M. Finding Moonshine. London: Fourth Estate, 2008.
Du Sautoy M. The Music of the Primes. London: Fourth Estate, 2003.
Eastaway R., Wyndham J. How Long Is a Piece of String? London: Robson Books, 2002.
Eastaway R., Wyndham J. Why Do Buses Come in Threes? London: Robson Books, 1998.
Ferguson K. The Music of Pythagoras. New York: Walker, 2008.
Fibonacci L. Fibonacci’s Liber Abaci. New York: Springer, 2002.
Gardner M. Martin Gardner's Mathematical Games. Washington: Mathematical Association of America, 2005.
Gowers T. Mathematics: A Very Short Introduction. Oxford: Oxford University Press, 2002.
Gullberg J. Mathematics: From the Birth of Numbers. New York: W. W. Norton, 1997.
Hidetoshi F., Rothman T. Sacred Mathematics. Princeton: Princeton University Press, 2008.
Hodges A. One to Nine. London: Short Books, 2007.
Hoffman P. The Man Who Loved Only Numbers. London: Fourth Estate, 1998.
Hogben L. Mathematics for the Million. London: George Allen & Unwin, 1936.
Hull T. Project Origami. Natick, Mass.: AK Peters, 2006.
Ifrah G. The Universal History of Numbers. Hoboken, N.J.: Wiley, 2000.