А ну-ка, догадайся! - Страница 13
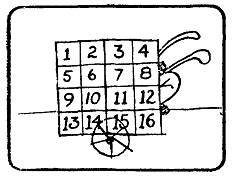
Начертите на листе бумаги эту матрицу 4х4 и перенумеруйте ее клетки числами от 1 до 16. Как вы сейчас убедитесь, я умею читать ваши мысли.

Обведите кружком любое число в матрице по своему усмотрению.
На рисунке обведено число 7, но вы можете выбрать другое число. Вычеркните все числа, которые стоят в одном столбце и в одной строке с обведенным числом.
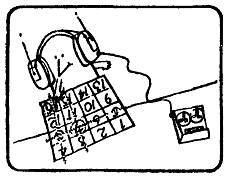
Обведите кружком любое из невычеркнутых чисел и вычеркните числа, стоящие с ним в одной строке и в одном столбце. Обведите кружком любое из оставшихся чисел и вычеркните те числа, которые стоят с ним в одной строке в в одном столбце. Наконец обведите кружком единственное оставшееся число.

Если вы все сделали правильно, то ваша матрица выглядит примерно так, как показано на рисунке. Сложите числа, обведенные кружками. Как вы их выбирали, мне не известно.

Готово? А теперь я назову вам их сумму. У вас получилось число… минуточку!.. 34. Правильно? Как я отгадал» сколько у вас получилось? Может быть, я действительно умею читать ваши мысли?
Почему начерченная нами матрица заставляет вас всегда выбирать четыре числа, дающие в сумме 34? Секрет этой матрицы прост и изящен. Над каждым столбцом матрицы 4х4 выпишем числа 1, 2, 3, 4, а слева от каждой строки выпишем числа 0, 4, 8, 12;

Эти 8 чисел называются генераторами, или образующими, магической матрицы. В каждую клетку впишем число, равное сумме двух генераторов, стоящих у той строки и того столбца, на пересечении которых расположена клетка. Вписав все числа, мы получим матрицу, клетки которой перенумерованы по порядку числами от 1 до 16:

Посмотрим, что произойдет, если мы выберем 4 числа в соответствии с описанной выше процедурой.
Она гарантирует, что никакие два обведенные кружками числа не окажутся в одной строке или в одном столбце, а поскольку каждое число в клетке равно сумме единственной и неповторимой пары образующих, то сумма четырех обведенных кружками чисел равна сумме 8 генераторов, которая, как нетрудно подсчитать, равна 34. Следовательно, сумма четырех выбранных чисел также должна быть равна 34.
Поняв, как устроена магическая матрица 4х4, вы без труда построите магическую матрицу любого порядка. Рассмотрим, например, приводимую ниже матрицу 6-го порядка с 12 генераторами. Они выбраны так, что числа в клетках матрицы кажутся случайными. Это еще более маскирует закон, по которому выписаны числа матрицы и придает ей еще большую таинственность.
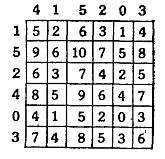
Сумма генераторов равна 30. Как бы ни выбирали в этой матрице 6 чисел, из которых никакие 2 не стоят в одной строке и в одном столбце, их сумма неизменно будет равна 30. Разумеется, эту сумму мы можем устанавливать по желанию.
Вы можете построить, например, магическую матрицу 10х10 с суммой генераторов, равной любому числу, которое покажется вам интересным, например «номер» текущего года или число лет, исполняющихся вашему доброму знакомому. Можно ли построить магические матрицы с отрицательными числами в некоторых клетках? Разумеется, можно.
Генератором магической матрицы может быть любое число, положительное или отрицательное, рациональное или иррациональное.
А можно ли построить магическую матрицу, в которой не сумма, а произведение выбранных чисел было бы равно заданному числу? Разумеется, можно, и это открывает перед нами еще одно направление исследований. Основная схема остается прежней, но нужное число равно не сумме, а произведению генераторов.
А что, если в клетки матрицы вписывать комплексные числа? И такое возможно, но мы предоставляем читателю разобраться в этом самостоятельно. Более подробные сведения о магических матрицах вы сможете почерпнуть в главе 2 («Фокусы с матрицами») моей книги «Математические головоломки и развлечения»[8].

Один адвокат, скопивший немалое состояние, собрал коллекцию из 11 старинных машин, каждую из которых знатоки оценивали примерно в 25 000 долларов.

После смерти адвокат оставил необычное завещание. По его воле 11 машин должны были быть разделены между 3 его сыновьями.
Половина машин должна была отойти старшему сыну, четверть — среднему и одна шестая — младшему.

Сыновья были не на шутку озадачены. Ну как можно разделить пополам 11 машин или, скажем, отделить от них четверть или одну шестую?

В разгар споров по поводу наследства мимо проезжала в своей новой спортивной машине знаменитый нумеролог миссис Зеро.
М-с Зеро. Хэлло, мальчики!
Что-то вид у вас не очень веселый. Может быть, я могу вам чем-нибудь помочь?

После того как братья объяснили миссис Зеро суть своих затруднений, она поставила свою машину рядом с 11 коллекционными машинами и выпорхнула из нее.
М-с Зеро. Сколько теперь машин перед вами?
Братья сосчитали — получилось 12 машин.

Затем миссис Зеро разделила 12 машин в соответствии с завещанием. Половину, или 6 машин, она отдала старшему сыну, четвертую часть, или 3 машины, — среднему сыну, и шестую часть, или 2 машины, — младшему сыну.
М-с 3еро. 6 плюс 3 плюс 2 — 11 машин. Одна машина лишняя, это моя машина.

Изящно впорхнув в свою машину, миссис Зеро дала газ и умчалась.
М-с Зеро. Всегда к вашим услугам, мальчики! Счет за консультацию я пришлю вам попозже.
Этот парадокс представляет собой современный вариант старинной арабской головоломки, в котором вместо лошадей речь идет о машинах. Вы можете по своему усмотрению изменять завещание старого чудака, варьируя число машин в оставшейся после него коллекции и доли наследства, причитающиеся его, сыновьям, следя лишь за тем, чтобы соблюдалось единственное условие: пополнив коллекцию еще одной машиной, сыновья получали возможность разделить наследство в соответствии с завещанием и вернуть «лишнюю» машину тому, кто любезно одолжил им ее.